Research Article
Shell model [1] has been one of the most successful
models to have explained evidence for magic numbers,
that has emerged from binding energy data. While
harmonic oscillator potential along with inclusion of
spin-orbit term has been very effective in obtaining
shell closures at magic numbers, actual energy level
sequencing as seen from experimental data is better
deduced by utilizing a rounded square well potential as
demonstrated by WS potential [2]. Even though square
well and harmonic oscillator potentials are included in
both under-graduate(UG) and post-graduate(PG)
nuclear physics courses [3], they are not dealt beyond
establishing the fact that magic numbers result due to .
splitting that gives rise to levels with higher j-values
corresponding to a particular N-oscillator getting clubbed
with those of a lower (N-1) oscillator. There is no
way to judge the magnitude of splitting due to this
spin-orbit coupling and hence different textbooks
[4, 5, 6] present varying energy level sequences which
could lead to difficulties while assigning the ground
state total angular momentum 𝐽 and spin-parities
(-1)ℓ for different nuclei. Another important lacuna
in the pedagogy of topics in this subject is the lack
of lab activities that enhance interaction with the
content. Our physics education research (PER) group
has been focusing on this much needed aspect and
have developed various experimental [7, 8, 9] and
simulation [10, 11, 12, 13] activities to supplement the
classroom lectures. With regard to single particle
energy level structure, we have solved the TISE for WS
potential along with spin-orbit term, utilizing matrix
methods technique employing sine wave basis in
Scilab [10]. In spite of the simplicity of sine basis, the
technique still requires determining integrals that appear
in the matrix elements numerically. This makes it
invariable to use a programming environment such as
Scilab. So as to overcome this limitation and keep ease
of simulating the problem using simple worksheet
environment, matrix methods numerical technique has
been replaced with Numerov method rephrased in matrix
form [14].
In this paper, we utilize model parameters obtained through optimization, while solving TISE using matrix methods [10], with respect to available experimental single particle energies [15]. The nuclear shell model with interaction potentials based on these model parameters, which are rephrased in appropriate choice of units, is described in Section II. A brief discussion on numerical Numerov method and its algorithm are given in Section III. The implementation details, for a typical example of 2040𝐶𝑎 using Gnumeric worksheet environment have been presented in a step by step approach in Appendix. The algorithm parameters are optimized to obtain convergence of single particle energies with those obtained using matrix methods [10] and final results are discussed in Section IV along with our initial attempts at implementation of a pilot study, by incorporating this tool into guided inquiry strategy (GIS) framework. Finally, we draw our conclusions in Section V.
The modeling methodology [16] has been described in great detail in our previous paper on Shell model simulation [10]. So, only a brief description of the potentials rephrased in MeV and fm units are given here. In shell model, a nucleus of mass number A, consisting of N neutrons and Z protons has been modeled by the assumption that each nucleon experiences a mean field of central potential type due to rest of the nucleons. Woods-Saxon (WS) potential, which has typically a rounded square well shape, is one of the successful mathematical formulations graphically represented in Figure 2 and is given by
| (1) |
where 𝑉0 is the depth of the well, given by [18]
𝑉0 =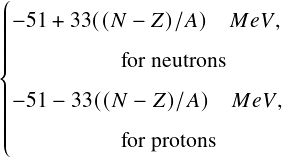 | (2) |
Here, r is the distance between two interacting nucleons,
R is the radius of the nucleus, empirically obtained as
N0𝐴1/3, with value of N0 being 1.28, a is surface
diffuseness parameter and is found to be 0.66 [10].]
Next, interaction of spin of nucleon with orbital angular
momentum of nucleon, as confirmed in experiments [17],
has been modeled by spin-orbit potential, as
| (3) |
Here, L.S =[𝑗(𝑗 +1)-ℓ(ℓ+1)-3/4]ℏ2, where ℓ is
orbital angular momentum quantum number, 𝑗 =ℓ+𝑠 is
total angular momentum quantum number and 𝑠 is spin
angular momentum quantum number given by 1/2 for
nucleons. The model parameters are 𝑉1 =-0.44𝑉0 [18]
and 𝑟0 = 0.90, a proportionality constant optimised
previously by our group [10] to obtain the right energy
level sequence. In our earlier work [10], the parameters 𝑟0
and 𝑎 were adjusted for a fixed value of N0 during
simulation to better match the experimental energy levels.
It was found that for 𝑟0 within range 0.86 - 0.95 and 𝑎
within range 0.66 - 0.67, the χ2 value comes out to be
minimum.
In case of protons, Coulomb potential also needs to be
considered and is given by
| (4) |
Here N𝑐 is the charge radius of the nucleus which in this case is considered to be equal to radius of nucleus R. The potential 𝑉𝑐(𝑟) is to be rephrased in MeV units. So, it is multiplied and divided by electron rest mass energy, [19] 𝑚𝑒𝑐2 =0.511 MeV to obtain
| (5) |
The radial TISE for central potentials is given by
| (6) |
where V(r) is net interaction potential experienced by a neutron or a proton and second term inside bracket, resulting from solution of θ-equation, is called as centrifugal potential 𝑉𝑐𝑓(𝑟) and μ is the reduced mass given by:
μ =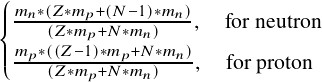 | (7) |
Here, 𝑚𝑝 =938.272 and 𝑚𝑛 = 939.565 are masses of proton and neutron respectively, in units of MeV/c2. The centrifugal potential 𝑉𝑐𝑓(𝑟) is rephrased in MeV units, by multiplying and dividing it by 𝑐2, so that
| (8) |
The value of ℏ𝑐=197.329 MeV-fm.
Consider TISE for a general potential V(r), given by
| (9) |
where
| (10) |
The advantage of this Eq. (9) is that it is linear in ’u’ having no first order derivative involved and is hence ideally suited for solving using Numerov method. The wave-function u(r) is expanded in Taylor series by explicitly retaining terms up-to 𝑂(ℎ4) and is obtained to an accuracy of 𝑂(ℎ6), [14]
𝑢(𝑟+ℎ)=𝑢(𝑟)+ℎ𝑢′(𝑟)+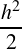 𝑢′′ (𝑟)+ 𝑢′′ (𝑟)+ | ||
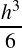 𝑢′′′ (𝑟)+ 𝑢′′′ (𝑟)+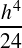 𝑢′′′′ (𝑟)+… 𝑢′′′′ (𝑟)+… | (11) |
Discretizing x in steps of h as:
𝑟1,𝑟2,…,𝑟𝑛-1,𝑟𝑛,𝑟𝑛+1,…,𝑟𝑁 .
Here, 𝑟𝑛 =𝑟1 +𝑛×ℎ
Now expressing 𝑢(𝑟𝑛 +ℎ) as 𝑢𝑛+1, so on and similarly,
𝑘(𝑟𝑛) as 𝑘𝑛, Eq. (11) can be written as
𝑢𝑛+1 =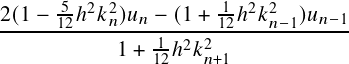 + + | ||
| 𝑂(ℎ6) | (12) |
Substituting from Eq. (10), 𝑘𝑛2 =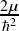 (𝐸-𝑉𝑛) into the
above, clubbing the terms containing 𝑉𝑛 and 𝐸, it can be
recast into the following form:
(𝐸-𝑉𝑛) into the
above, clubbing the terms containing 𝑉𝑛 and 𝐸, it can be
recast into the following form:
- 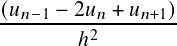 + + | ||
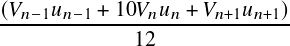 | (13) | |
=𝐸 | (14) |
One has to keep in mind that whatever may be the potential, if wave-function were to be normalised, it should tend to 0 as x tends to ±∞. This implies, one has to choose the region of interest (RoI) large enough to ensure that the wave-function dies down to zero in either direction. That is, x values are limited to an interval such as [𝐿1,𝐿2], such that 𝑢 goes to 0 at both ends of the interval. More specifically,
| (15) |
and
| (16) |
Expanding the above equation for all intermediate points (𝑗 = 2,3,…,𝑁 -1), one will get a matrix equation as
| (17) |
where in, 𝑢 is a column vector (𝑢2,…,𝑢𝑛-1,𝑢𝑛,𝑢𝑛+1,…,𝑢𝑁-1 ),
Similarly, V is a column vector (𝑉2,…,𝑉𝑛-1,𝑉𝑛,𝑉𝑛+1,…,𝑉𝑁-1 ),
but is converted into a diagonal matrix with these values
along its central diagonal. Matrices A and B are given
by
| (18) |
and
| (19) |
where 𝐼𝑝 represents a matrix consisting of 1’s along 𝑝𝑡ℎ
diagonal and zeros elsewhere, here 𝑝 can be positive
(above the main diagonal, i.e 𝐼1), zero (the main
diagonal, i.e 𝐼0) or negative (below the main diagonal, i.e
𝐼-1).
Multiplying Eq. (17) by B-1 on both sides, gives TISE as
a matrix equation, utilising Numerov method,
| (20) |
with an error of 𝑂(ℎ6).
Notice that a factor of 𝑐2 is introduced in both numerator
and denominator to ensure the units are in 𝑀𝑒𝑉 and 𝑓𝑚
as required in nuclear physics.
This is the final equation that needs to be solved
numerically to get energy eigen-values and eigen-functions
of a particle interacting with a given potential V(r). The
imposition of boundary conditions as 𝑢1 =𝑢𝑁 =0 is
equivalent to embedding the potential of interest,
inside an infinite square well potential. Finally,
(𝑁-2)×(𝑁 - 2) sub-matrices of A and B are utilised to
solve for the energy eigen-values and their corresponding
eigen-vectors.
A step by step approach to determining the single particle energies for protons of 2040𝐶𝑎 is presented.
=($J$8*($J$8+1)*$J$14^2*
($A22^(-2)))/(2*$J$13)
=$F$9*(1+$C22)^(-1)
=-$F$14*$F$13^2*$J$16*$C22*
$E22*($F$10*$A22)^(-1)
where, the L.S term in cell J16 is calculated by formula:
=$J$9*($J$9+1)-$J$8*
($J$8+1)-3/4
=$B$14*0.511*2.839*
(3*$B$15^2-$A22^2)/(2*$B$15^3)
in cell G22 up-to radius ’R’ of the nucleus. After that in cell G65, type the formula:
=0.511*2.839*$A65^(-1)*$B$14
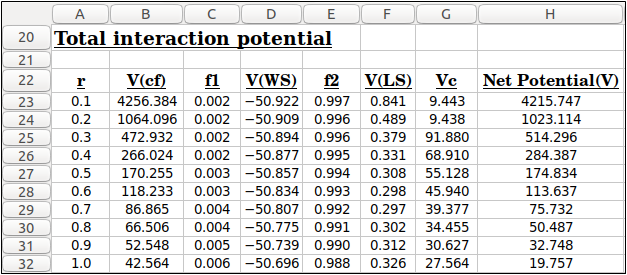
which gives the Coulomb potential outside the range of nuclear radius.
=$B22+$D22+$F22+$G22
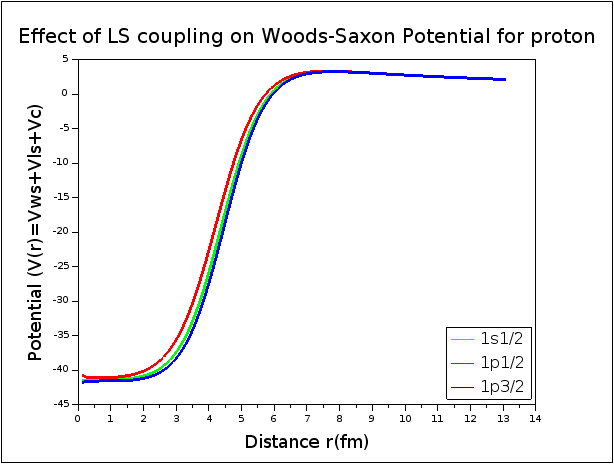
Figure (2a) consists of the potential values for the few r values and Figure (2b) shows the plot of Woods-Saxon potential of 1𝑠1/2,1𝑝1/2 and 1𝑝3/2 states for proton, showing that inclusion of angular momentum on L.S coupling affects the Woods-Saxon potential.
=if($A4=B$3,10/12,
if($A4+1=B$3,1/12,
if($A4-1=B$3,1/12,0)))
This is repeated by dragging across till EB4 and then downwards to EB134 to obtain the tridiagonal B-matrix as shown in Figure (3a).

=minverse(’Sheet 2’!B4:EB134)
press Ctrl+Shift+Enter keys together to
obtain matrix-𝐵-1 as in Figure (3b).
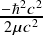 from cell J15 of Sheet 1. Then, in
cell B7, the formula is given as
from cell J15 of Sheet 1. Then, in
cell B7, the formula is given as
=if($A7=B$6,(-2*$D$3/$D$4^2),
if($A7+1=B$6,($D$3/$D$4^2),
if($A7-1=B$6,($D$3/$D$4^2),0)))
and dragged appropriately to generate the required values as shown in Figure (3c).
=mmult(Sheet3!B4:EB134,’Sheet 4’!
B7:EB137)
The obtained matrix is shown in Figure (3d).
=if($A4=B$3,’Sheet 1’!$H22,0)
so that only diagonal elements get populated as those of net potential values from Sheet 1 and seen in Figure (3e).
=(Sheet5!B4:EB134+’Sheet 6’
!B4:EB134)
and dragging the formula to fill values from B4: EB134 as seen in Figure (3f).
=eigen(Sheet7!B4:EB134)
and all the three keys Ctrl+Shift+Enter pressed together. The resultant values are shown in Figure (4a) and (4b).
Starting from ℓ =0, s-states, in which case 𝑗 =0.5 alone exists
for ℓ = 1, p-states, we have two values of j: 𝑗 =0.5 and 𝑗 =1.5.
Similarly for ℓ =2, d-states, 𝑗 takes values 1.5 and 2.5 , and so on.
This is continued till no bound states are obtained for particular ℓ and 𝑗 values.
In this section, we will first validate our approach to
obtain energy eigen-values and eigen-functions using
Woods-Saxon potential with . coupling for both
neutron and proton for doubly magic nucleus 2040𝐶𝑎.
This is done by comparing our results with available
experimental results and those obtained numerically by using matrix method with Fourier basis [10] for different
angular momentum values ℓ and j. The results are
tabulated in Table 1.
| States | Proton states (MeV) | States | Neutron states (MeV)
| ||||
| Exp. | Numerical values | Exp. | Numerical values
| ||||
| Ref[15] | Ref[10] | Current | Ref[15] | Ref[10] | Current | ||
| 1𝑠1/2 | … | -30.49 | -30.49 | 1𝑠1/2 | … | -38.90 | -38.90 |
| 1𝑝3/2 | … | -21.68 | -21.68 | 1𝑝3/2 | … | -29.55 | -29.55 |
| 1𝑝1/2 | … | -19.04 | -19.04 | 1𝑝1/2 | … | -26.99 | -26.99 |
| 1𝑑5/2 | -15.07 | -12.19 | -12.19 | 1𝑑5/2 | -22.39 | -19.54 | -19.54 |
| 2𝑠1/2 | -10.92 | -8.14 | -8.14 | 2𝑠1/2 | -18.19 | -15.54 | -15.54 |
| 1𝑑3/2 | -8.33 | -6.85 | -6.85 | 1𝑑3/2 | -15.64 | -14.28 | -14.28 |
| 1𝑓7/2 | -1.09 | -2.33 | -2.33 | 1𝑓7/2 | -8.36 | -9.15 | -9.15 |
| 2𝑝3/2 | 0.69 | 1.00 | 1.00 | 2𝑝3/2 | -5.84 | -5.42 | -5.42 |
| 2𝑝1/2 | 2.38 | 2.94 | 2.94 | 2𝑝1/2 | -4.20 | -3.10 | -3.10 |
| 1𝑓5/2 | 4.96 | 5.37 | 5.37 | 1𝑓5/2 | -1.56 | -1.19 | -1.20 |
The obtained energy eigen values are in good agreement
with experimental energy values of different neutron and
proton single particle states for step size of h=0.1 thus
validating our approach. One can observe from the Table
1, that while the numerical or simulated values are below
than those of experimental ones for lower proton and
neutron states, the trend is opposite for higher states. This
discrepancy arises because the optimization algorithm, in
its attempt to minimize χ2, tends to find values close to
the expected ones.
The distance parameter ’r’ is discretized as per step size
’h’ and its values are varied from 𝑟 =0.1 to 𝑟 =3N, where
N =N0𝐴(1/3). Therefore, it is necessary to vary the size
of matrix ‘N’ for different A values for a chosen step size
‘h’. This simulation activity can be utilised as a tool to
apply GIS[20] of constructivist approach to learning and
has been done as follows:
The students have been taken through following six step process of GIS. All steps were implemented on online Moodle platform [21] during COVID-19 lockdown of university.
Initiation: The matrix Numerov technique was already introduced before, for solving the harmonic oscillator potential. Next, it has been applied to solve for single particle energies of both neutrons and protons, as dealt with in this paper, for Woods-Saxon potential with spin-orbit potential. This has been explained and also demonstrated in two successive lab sessions.
Selection: The students were made to explore the binding energy and separation energies curves that they have plotted in previous sessions, to identify various double magic nuclei suitable for study. The doubly magic nuclei from 816𝑂 to 82208𝑃𝑏 were selected. The determination of single particle proton and neutron energy level sequences for six double magic nuclei, are assigned to students by dividing them into 12 groups. Each group is expected to obtain the energy level sequence of either neutrons or protons for the assigned nuclei by carefully following the simulation procedure.
Presentation: The students in each group could be asked to present their findings to the rest of the class so that everyone gets to know each other’s experience. Even though all the groups could get to expected level sequence by following the steps correctly, some of the students have not ensured reduction of step-size systematically. Hence, they have come up with lower accuracy for energies even though they obtained correct level sequence. They have been guided accordingly.
Exploration: The collective findings were shared with entire class and they were asked to explore nuclei adjacent to the magic numbers with one neutron or proton more and find out ground state 𝐽π configuration for each of them.
Formulation: They were expected to formulate their findings based on right choice of level sequence and also figure out what they would get if they followed the level sequence given in their prescribed textbook [4].
Collection: To understand variation of energy level structure with mass number, students were asked to plot the compiled energy data for protons and neutrons as a function of mass number A. They were able to obtain plots similar to what have been presented in [10].
Assessment: They have assessed their formulated ground state angular momentum and spin configurations based on the experimental findings and thus validated their outcomes. They could be further asked to obtain the ground state configurations of nuclei slightly away from magic nuclei till the results obtained are in variance with those from experiments as an excercise.
The results matching with experimentally available values
[15] were obtained for step-size ’ℎ =0.1’ for doubly
magic nuclei from 816𝑂 to 82208𝑃𝑏. The value of
N (to solve N × N matrix) for each of these nuclei
are obtained as 96,131,138, 145, 177, 194 and 229
respectively. The obtained energy level sequences
for neutrons and protons of these nuclei are given
separately in tabular form in Tables 2 and 3. The
first four levels, 1𝑠1/2,1𝑝3/2,1𝑝1/2 ad 1𝑑5/2 are not
shown, as there are no discrepancies found in the
ordering of these levels across the periodic table due to
our simulation. The numerically obtained energy
values are found to match to two decimal places with
those obtained using the matrix method approach
[10]. The χ2-value defined as relative mean-squared
error
| (21) |
These are determined w.r.t experimental [15] and are
shown in Tables. In Tables 2 and 3, energy level sequence
obtained for lighter nuclei 16𝑂 to 56𝑁𝑖 are shown in first
column and that for 100𝑆𝑛 to 82208𝑃𝑏 in last column. It can
be observed that the energy level sequence for lighter
nuclei is different than that for heavier ones. This
might be because the effect of spin-orbit coupling
is different for light nuclei and heavy nuclei which
results into the change in internal structure. Also, the
amount of splitting in the energy levels is different for
different mass numbers. The observed discrepancies
in energy sequence are highlighted in red colour.
The discrepancy in level sequence for lighter nuclei w.r.t
heavy nuclei is highlighted in blue colour in both tables;
i.e for neutron and proton states. Further, it is found
that in most of the textbooks at UG and PG level
[4, 5, 6, 18, 22, 23], energy level sequence given is
different. Also, there is only single energy level sequence
given for both neutrons and protons, and that too common
for all mass ranges. But according to our calculations as
well as Bohr and Mottelson book, there should be
different energy level sequences for nuclei across the
periodic table.
| States | Numerical energy values(MeV) | States | |||||
| 816𝑂 | 20 48 𝐶𝑎 | 28 56 𝑁𝑖 | 50 100 𝑆𝑛 | 50 132 𝑆𝑛 | 82 208 𝑃𝑏 | ||
| 2𝑠1/2 | -3.03 | -14.19 | -20.51 | -29.27 | -25.57 | -30.90 | 1𝑑3/2 |
| 1𝑑3/2 | 2.11 | -13.58 | -20.35 | -28.34 | -24.46 | -29.67 | 2𝑠1/2 |
| 1𝑓7/2 | … | -8.33 | -14.96 | -24.04 | -20.78 | -26.74 | 1𝑓7/2 |
| 2𝑝3/2 | … | -4.90 | -10.56 | -20.08 | -18.07 | -25.07 | 1𝑓5/2 |
| 1𝑓5/2 | … | -1.87 | -8.41 | -19.75 | -17.15 | -23.59 | 2𝑝3/2 |
| 2𝑝1/2 | … | -3.00 | -8.32 | -18.19 | -16.06 | -22.87 | 2𝑝1/2 |
| 1𝑔9/2 | … | 1.16 | -5.25 | -16.07 | -14.01 | -21.20 | 1𝑔9/2 |
| 2𝑑5/2 | … | … | -1.70 | -10.01 | -9.79 | -18.50 | 1𝑔7/2 |
| 3𝑠1/2 | … | … | -0.94 | -11.17 | -9.76 | -17.20 | 2𝑑5/2 |
| 1𝑔7/2 | … | … | 3.52 | -8.36 | -7.99 | -15.76 | 2𝑑3/2 |
| 2𝑑3/2 | … | … | … | -9.05 | -7.74 | -15.44 | 3𝑠1/2 |
| 1ℎ11/2 | … | … | … | -7.69 | -6.83 | -15.24 | 1ℎ11/2 |
| 2𝑓7/2 | … | … | … | -2.95 | -0.94 | -11.28 | 1ℎ9/2 |
| 3𝑝3/2 | … | … | … | -1.53 | -2.61 | -10.64 | 2𝑓7/2 |
| 3𝑝1/2 | … | … | … | -0.53 | -0.57 | -8.90 | 1𝑖13/2 |
| 1ℎ9/2 | … | … | … | 0.59 | -1.34 | -8.45 | 3𝑝3/2 |
| … | … | … | … | … | 0.03 | -8.36 | 2𝑓5/2 |
| … | … | … | … | … | … | -7.55 | 3𝑝1/2 |
| … | … | … | … | … | … | -4.04 | 2𝑔9/2 |
| … | … | … | … | … | … | -3.49 | 1𝑖11/2 |
| … | … | … | … | … | … | -2.24 | 1𝑗15/2 |
| … | … | … | … | … | … | -2.07 | 3𝑑5/2 |
| … | … | … | … | … | … | -1.41 | 4𝑠1/2 |
| … | … | … | … | … | … | -1.01 | 2𝑔7/2 |
| … | … | … | … | … | … | -0.82 | 3𝑑3/2 |
| χ2 | 0.24 | 1.18 | 0.09 | 0.06 | 0.03 | 0.06 | … |
| States | Numerical energy values(MeV) | States |
|||||
|
| 816𝑂 | 20 48 𝐶𝑎 | 28 56 𝑁𝑖 | 50 100 𝑆𝑛 | 50 132 𝑆𝑛 | 82 208 𝑃𝑏 |
|
| 2𝑠1/2 | -0.21 | -15.18 | -10.71 | -14.25 | -26.11 | -24.16 | 1𝑑3/2 |
| 1𝑑3/2 | 4.82 | -14.55 | -10.60 | -13.05 | -24.61 | -22.26 | 2𝑠1/2 |
| 1𝑓7/2 | … | -9.75 | -5.89 | -9.83 | -21.70 | -20.56 | 1𝑓7/2 |
| 2𝑝3/2 | … | -4.98 | -1.56 | -5.58 | -18.24 | -18.37 | 1𝑓5/2 |
| 2𝑝1/2 | … | -2.38 | 0.54 | -5.14 | -16.97 | -16.25 | 2𝑝3/2 |
| 1𝑓5/2 | … | -1.71 | … | -3.56 | -15.58 | -15.36 | 2𝑝1/2 |
| 1𝑔9/2 | … | 0.40 | … | -2.43 | -14.77 | -15.18 | 1𝑔9/2 |
| 2𝑑5/2 | … | … | … | 3.92 | -9.37 | -11.71 | 1𝑔7/2 |
| 1𝑔7/2 | … | … | … | 2.55 | -9.10 | -9.89 | 2𝑑5/2 |
| 1ℎ11/2 | … | … | … | … | -7.32 | -9.29 | 1ℎ11/2 |
| 3𝑠1/2 | … | … | … | … | -6.56 | -8.09 | 2𝑑3/2 |
| 2𝑑3/2 | … | … | … | … | -6.43 | -7.57 | 3𝑠1/2 |
| 2𝑓7/2 | … | … | … | … | -1.18 | -4.26 | 1ℎ9/2 |
| 1ℎ9/2 | … | … | … | … | 0.330 | -3.26 | 2𝑓7/2 |
| … | … | … | … | … | … | -2.95 | 1𝑖13/2 |
| … | … | … | … | … | … | -0.37 | 2𝑓5/2 |
| … | … | … | … | … | … | -0.28 | 3𝑝3/2 |
| χ2 | 1.53 | 0.31 | 0.48 | 0.25 | 0.03 | 0.11 | … |
Next, 𝐽π assignments for nuclei near to doubly
magic nuclei in mass range equal to and less than
82208𝑃𝑏 based on our simulation, which match with
experimentally[15] available energy sequence, are
tabulated. These assignments are compared with those
calculated using energy level sequence given in usually
referred textbook Introductory Nuclear Physics by
Kenneth Krane[4] by considering only the energy
level sequence of lighter nuclei, and are shown in
Table 4. The discrepancies in spin assignments are
highlighted in blue colour. These discrepancies are also
observed in other textbooks [5, 6, 17, 22, 23] as
well.
| Nuclei | Neutron states | Nuclei | Proton states | ||||||||
|
| Ref.[4 ] | Current work | Ref.[4] | Current work | |||||||
| 817𝑂 | 1𝑑5/2 | 1𝑑5/2 | 9 16 𝐹 | 1𝑑5/2 | 1𝑑5/2 | ||||||
| 2041𝐶𝑎 | 1𝑓7/2 | 1𝑓7/2 | 2140𝑆𝑐 | 1𝑑3/2 | 1𝑑3/2 | ||||||
| 2049𝐶𝑎 | 2𝑝3/2 | 2𝑝3/2 | 2148𝑆𝑐 | 1𝑓7/2 | 1𝑓7/2 | ||||||
| 2857𝑁𝑖 | 2𝑝3/2 | 2𝑝3/2 | 29 56 𝐶𝑢 | 1𝑓 7/2 | 2𝑝3/2 | ||||||
| 50101𝑆𝑛 | 1𝑔7/2 | 2𝑑5/2 | 51100𝑆𝑏 | 1𝑔9/2 | 2𝑑5/2 | ||||||
| 50133𝑆𝑛 | 1ℎ9/2 | 2𝑓7/2 | 51132𝑆𝑏 | 1ℎ11/2 | 2𝑑3/2 | ||||||
| 82209𝑃𝑏 | 2𝑔9/2 | 1𝑖11/2 | 83208𝐵𝑖 | 1ℎ9/2 | 2𝑓7/2 | ||||||
Hence, from our observations, the level sequence for lighter mass range and heavy mass range nuclei can be modified accordingly so as to provide students with data consistent with experiments.
The time-independent Schrödinger equation (TISE) for a nucleus modeled using Woods-Saxon potential along with spin-orbit coupling term has been solved numerically by choosing Matrix Numerov method. The main advantage of matrix Numerov method is that it can be easily extended to any arbitrary potential of interest. It is implemented in Gnumeric worksheet environment to obtain numerical solutions of single-particle neutron and proton states for doubly magic nuclei 2040𝐶𝑎. Then, using guided enquiry strategy, a Constructivist approach, students were grouped and encouraged to obtain energy level sequences for other doubly magic nuclei up-to 𝑍 =82, i.e 816𝑂, 2048𝐶𝑎, 2856𝑁𝑖, 50100𝑆𝑛, 50132𝑆𝑛 and 82208𝑃𝑏. Based on these obtained level structures, students obtained ground state total angular momentum and spin assignment for various nuclei close to doubly magic nuclei successfully and it could easily be extended to test the limits of validity.
[1] E. Meyer, Am. J. Phys. 36, 250 (1968).
https://doi.org/10.1119/1.1974490
[2] R. D. Woods and D. S. Saxon, Phys. Rev. 95, 577
(1954).
https://doi.org/10.1103/PhysRev.95.577
[3] https://www.ugc.ac.in/pdfnews
/7870779_B.SC.PROGRAM-PHYSICS.pdf.
[4] S. K. Krane, Introductory Nuclear Physics (Jon
Wiley & Sons, New York, 1988).
https://www.wiley.com/en-us/Introductory+Nuclear+Physics%2C+3rd+Edition-p-9780471805533
[5] S. N. Ghoshal, Nuclear Physics (S. Chand
Publishing, 1997).
https://books.google.co.in/books?id=fkqHNMd_248C
&printsec=copyright#v=onepage&q&f=false
[6] S. S. M. Wong, Introductory Nuclear Physics,
(John Wiley & Sons, New York, 1998).
https://onlinelibrary.wiley.com/doi/book/10.1002
/9783527617906
[7] J. Bhagavathi, S. Gora, V.V.V. Satyanarayana,
O.S.K.S. Sastri, and B.P. Ajith, Phys. Educ. 36, 1
(2020).
https://csparkresearch.in/assets/pdfs/gammaiapt.pdf
[8] B.P. Jithin, V.V.V. Satyanarayana, S. Gora, O. S.
K. S. Sastri and, B.P. Ajith, Phys. Educ. 35, 1 (2019).
https://csparkresearch.in/assets/pdfs/alpha2.pdf
[9] S. Gora, B.P. Jithin, V.V.V. Satyanarayana,
O.S.K.S. Sastri, and B.P. Ajith, Phys. Educ. 35, 1
(2019).
https://www.semanticscholar.org/paper/Alpha-Spectrum-of-212-Bi-Source-Prepared-using-of-3-Gora-Jithin/a1998cfee897c57968e08be30a45396fae757e90
[10] A. Sharma, S. Gora, J. Bhagavathi, and O.S.K.
Sastri, Am. J. Phys. 88, 576 (2020).
https://doi.org/10.1119/10.0001041
[11] O.S.K.S Sastri, Aditi Sharma, Jyoti Bhardwaj,
Swapna Gora, Vandana Sharda and Jithin B.P, Phys.
Educ., 1 (2019).
https://www.researchgate.net/publication/348555315
_Numerical_Solution_of_Square_Well_Potential_With
_Matrix_Method_Using_Worksheets
[12] A. Sharma and O.S.K.S. Sastri, Eur. J. Phys. 41,
055402 (2020).
https://iopscience.iop.org/article/10.1088/1361-6404/ab988c/meta
[13] O.S.K.S. Sastri, A. Sharma, S. Awasthi, A.
Khachi, and L. Kumar, Phys. Educ. 36, 1 (2019).
http://www.physedu.in/pub/2020/PE20-09-673
[14] M. Pillai, J. Goglio, and T.G. Walker, Am. J. Phys.
80, 1017 (2012).
https://doi.org/10.1119/1.4748813
[15] N. Schwierz, I. Wiedenhover, and A. Volya,
arXiv:0709.3525 [nucl-th] (2007).
https://arxiv.org/abs/0709.3525
[16] D. Hestenes, Am. J. Phys. 55, 440 (1987).
https://doi.org/10.1119/1.15129
[17] K.L.G. Heyde, The Nuclear Shell Model,
Springer, Berlin, Heidelberg (1994).
https://doi.org/10.1007/978-3-642-79052-2_4
[18] A. Bohr and B.R. Mottelson, Nuclear Structure,
World Scientific, Singapore (1998).
https://doi.org/10.1142/3530
[19] https://nukephysik101.wordpress.com
/tag/runge-kutta/ for solving Woods-Saxon potential
using Runge-Kutta method.
[20] "Guided inquiry process".
https://www.michiganseagrant.org
/lessons/teacher-tools/guided-inquiry-process/
[21] https://saivyasa.in/moodle/
message/index.php?id=2
[22] A.P. Arya, Fundamentals of Nuclear Physics,
Allyn and Bacon, Inc., Boston (1966).
https://archive.org/details/fundamentalsofnu0000arya
[23] R. Casten and R.F. Casten, Nuclear Structure
from a Simple Perspective, (Oxford University Press
on Demand, 2000.)
https://homel.vsb.cz/ãle02/Physics/RFCasten-NuclearStructureFromASimplePerspective.pdf
[© 2024 Shikha Awasthi, et al.] This is an Open Access article published in "Graduate Journal of Interdisciplinary Research, Reports & Reviews" (Grad.J.InteR3) by Vyom Hans Publications. It is published with a Creative Commons Attribution - CC-BY4.0 International License. This license permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
____________________________________________________________________________________________